Traitement d’images (partie 6: Filtres & Convolution)

• Partie 1: L’image numérique
• Partie 2: Les histogrammes
• Partie 3: Seuillage d’image
• Partie 4: Transformations de base
• Partie 5: Transformations morphologiques
• Partie 6: Filtres & Convolution
• Partie 7: Les réseaux de neurones à convolution (CNN)

Dans le précédent chapitre nous avons fait sans le savoir un premier pas vers les filtres. Ce principe de la petite fenêtre glissante nous allons le généraliser mais surtout aller plus loin en y ajoutant des opérations sur les valeurs de pixel. Nous allons donc aborder dans cet article une famille de filtre très utilisée par tous les logiciels de retouches (comme Photoshop ou Gimp). En fait et pour aller plus loin (sans non plus pour autant « sploiler » les articles suivants) ce principe de convolution va aussi être très utilisés par les réseaux de neurones (Deep Learning) … mais nous verrons cela plus tard. Focalisons nous tout d’abord sur le principe de filtre et plus précisément de convolution.

Principe de convolution

Comme je l’ai précisé en introduction nous allons garder le principe de la fenêtre glissante qui va donc parcourir toute l’image de haut en bas et de gauche à droite (même si en réalité l’ordre et le sens n’ont pas d’importance, mais c’est plus simple à visualiser pour la compréhension). Cette fenêtre glissante s’appelle le kernel (on voit bien ici la racine mathématique du concept). On trouve aussi les terminologies de noyau de convolution ou même de masque de convolution.

Etape N°1

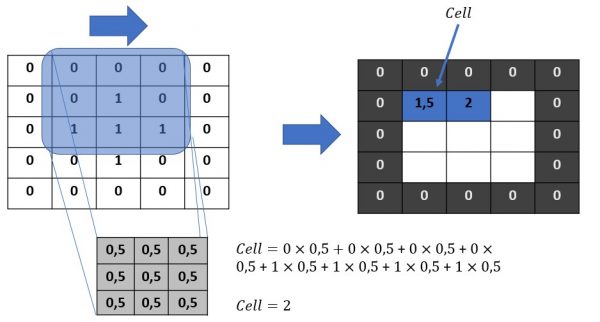
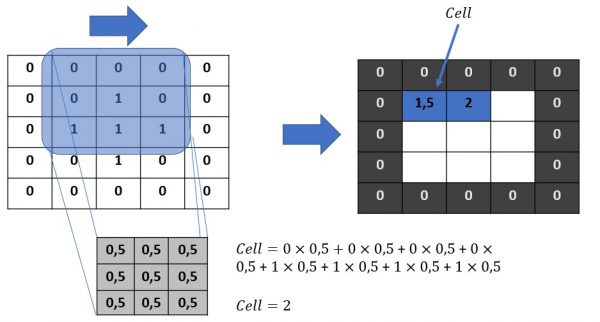
Le principe est donc très simple. On superpose le kernel sur le coin gauche de la matrice de l’image, comme ci-dessous. Pour information le kernel est la matrice avec des seules valeurs 0,5 dans l’illustration ci-dessous. Ensuite nous allons multiplier chaque nombre superposé puis additionner le tout. Le résultat prendra sa place naturellement comme cela est montré dans la figure.

Notre premier pixel est donc recalculé, on peut passer au suivant. Pour ce faire on déplace juste le kernel d’un rang. Puis on refait exactement la même opération.

Etapes suivantes

On effectue cela bien sur pour tous les pixels de l’image à filtrer. On doit obtenir par ce procédé simple une nouvelle image (matrice) filtrée. Ce procédé est vraiment efficace d’une part et de plus très peu couteux pour la machine car seules des additions & multiplications sont effectuées. Nous venons de faire ce que l’on appelle un produit de convolution. Cette opération est de plus une application bilinéaire, associative et commutative.

Une petit détail demeure quand même! Avez-vous remarqué qu’il était impossible de calculer les pixels du bord ?

Heureusement les bords ne comprennent que rarement des pixels importants, et puis ils sont peu nombreux par rapport au reste de l’image. Il existe plusieurs stratégies donc pour remplir ces bords. On peut simplement les laisser à zéro, répliquer les valeurs à coté, calculer une moyenne des pixels alentours, etc.

Si vous avez compris le principe, vous allez maintenant en voir l’intérêt. En fait la clé du filtrage se trouve dans la création du noyau. Heureusement les mathématiciens ont déjà travaillé pour nous en fournissant des noyaux tout fait pour effectuer bon nombre d’opérations de filtrage. Nous allons en passer quelques uns en revue.

Pour mieux se familiariser avec ce concept (si quelqu’un à encore un doute), allez sur ce site https://setosa.io/ev/image-kernels/ vous pourrez jouer avec les filtres et voir directement les résultats.

Convolution avec Python

Nous n’allons pas utiliser de librairies toutes faites comme il en existe. Afin d’illustrer le principe que nous voyons de voir nous allons directement jouer avec les matrices/pixels. Nous utiliserons donc la librairie SciPy pour les opérations matricielles de convolution.

Commençons par importer quelques librairies et ajoutons une petite fonction de visualisation:

import numpy as np
from skimage import data
import matplotlib as plt
from scipy import signal
from matplotlib.pyplot import imshow, get_cmap
import matplotlib.pyplot as plt
def displayTwoBaWImages(img1, img2):
  _, axes = plt.subplots(ncols=2)
  axes[0].imshow(img1, cmap=plt.get_cmap('gray'))
  axes[1].imshow(img2, cmap=plt.get_cmap('gray'))

Créons maintenant une image toute simple en noir et blanc:

image_test = np.array([[0,0,0,0,0], 
                       [0,0,1,0,0], 
                       [0,1,1,1,0], 
                       [0,0,1,0,0], 
                       [0,0,0,0,0]])
imshow(image_test, 
       cmap=get_cmap('gray'))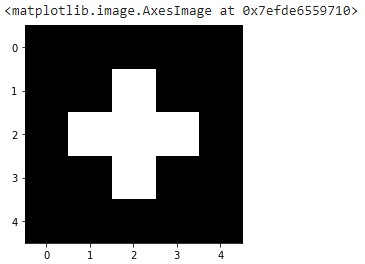

Créons un noyau de convolution très simple

kernel = np.ones((3,3), np.float32)/2

Demandons à Scipy de faire le produit de convolution

imgconvol = signal.convolve2d(image_test, 
                              kernel, 
                              mode='same',
                              boundary='fill', 
                              fillvalue=0)
displayTwoBaWImages(image_test, imgconvol)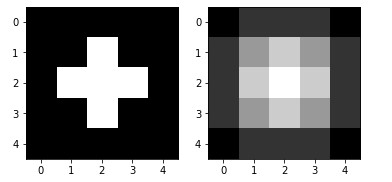

Si on regarde l’image (sa matrice) :

array([[0. , 0.5, 0.5, 0.5, 0. ],
       [0.5, 1.5, 2. , 1.5, 0.5],
       [0.5, 2. , 2.5, 2. , 0.5],
       [0.5, 1.5, 2. , 1.5, 0.5],
       [0. , 0.5, 0.5, 0.5, 0. ]])

Ce filtre a en quelque sorte créé un flou sur l’image de base comme on peut le voir.

Voyons d’autres filtres maintenant.

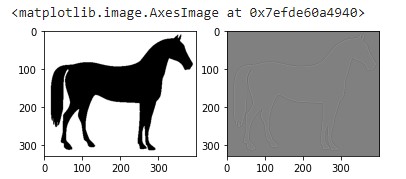
Détection de contours

Le noyau de convolution qui permet de détecter les contours est une matrice 3×3 toute simple :

kernel_contour = np.array([[0,1,0], 
                       [1,-4,1], 
                       [0,1,0]])

Appliquons le filtre de convolution comme précédemment :

imgconvol = signal.convolve2d(image, 
                              kernel_contour, 
                              boundary='symm', 
                              mode='same')
displayTwoBaWImages(image, imgconvol)
imshow(imgconvol, cmap=get_cmap('gray'))

Résultant plutôt bluffant n’est-ce pas ?

Augmentation de contraste

Le noyau de convolution est maintenant une matrice 5×5:

kernel_inccontrast = np.array([[0,0,0,0,0], 
                               [0,0,-1,0,0], 
                               [0,-1,5,-1,0], 
                               [0,0,-1,0,0], 
                               [0,0,0,0,0]])

array([[ 0,  0,  0,  0,  0],
       [ 0,  0, -1,  0,  0],
       [ 0, -1,  5, -1,  0],
       [ 0,  0, -1,  0,  0],
       [ 0,  0,  0,  0,  0]])

imgcontrast = signal.convolve2d(data.camera(), 
                              kernel_inccontrast, 
                              boundary='symm', 
                              mode='same')
displayTwoBaWImages(data.camera(), imgcontrast)

Flouttage

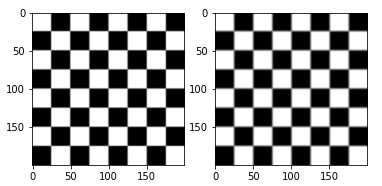
kernel = np.array([[0,0,0,0,0], 
                    [0,1,1,1,0], 
                    [0,1,1,1,0], 
                    [0,1,1,1,0], 
                    [0,0,0,0,0]])
img = signal.convolve2d(data.checkerboard(), 
                        kernel, 
                        boundary='symm', 
                        mode='same')
displayTwoBaWImages(data.checkerboard(), img)

Renforcement de bords

kernel = np.array([[0,0,0], 
                   [-1,1,0,], 
                   [0,0,0,]])
img = signal.convolve2d(data.camera(), 
                        kernel, 
                        boundary='symm', 
                        mode='same')
displayTwoBaWImages(data.camera(), img)

Conclusion

Il existe bon nombre de noyaux de convolution déjà fournis et qui permettent comme nous venons de le voir d’effectuer des opérations sur les images. Nous verrons dans un prochain article comment les réseaux de neurones à convolution vont trouver et combiner des filtres de convolution pour détecter des formes plus complexes.

Benoit Cayla

Ingénieur en informatique avec plus de 20 ans d’expérience dans la gestion et l’utilisation de données, Benoit CAYLA a mis son expertise au profit de projets très variés tels que l’intégration, la gouvernance, l’analyse, l’IA, la mise en place de MDM ou de solution PIM pour le compte de diverses entreprises spécialisées dans la donnée (dont IBM, Informatica et Tableau). Ces riches expériences l’ont naturellement conduit à intervenir dans des projets de plus grande envergure autour de la gestion et de la valorisation des données, et ce principalement dans des secteurs d’activités tels que l’industrie, la grande distribution, l’assurance et la finance. Également, passionné d’IA (Machine Learning, NLP et Deep Learning), l’auteur a rejoint Blue Prism en 2019 et travaille aujourd’hui en tant qu’expert data/IA et processus. Son sens pédagogique ainsi que son expertise l’ont aussi amené à animer un blog en français (datacorner.fr) ayant pour but de montrer comment comprendre, analyser et utiliser ses données le plus simplement possible.