Traitement d’images (partie 7: Les Réseaux de neurones à convolution – CNN)

Nous voici donc arrivé à la fin de cette série sur le traitement d’image. Et comment mieux terminer une série comme celle-ci qu’en ouvrant sur un autre monde … celui des réseaux de neurones. Bien entendu impossible de traiter en 1 seul article les réseaux de neurones, et encore moins dans le détails les réseaux de neurones à convolution (ou CNN). Néanmoins, je vais essayer de vous initier à cette technique que l’on retrouve (sans toujours le savoir) un peu partout dés lors que l’on traite des images.

Cet article est la suite logique de l’article précédent et par du principe que vous avez de bonnes notions sur les Réseaux de Neurones Artificiels (ANN). Si ce n’est pas le cas, vous pouvez aussi lire cet article (tutoriel) que j’avais écris sur le Titanic. Bien sur d’autres articles spécifiques aux Réseaux de neurones, ne vont pas tarder à apparaitre sur ce site 😉

Qu’est-ce qu’un CNN ?

Très simplement un CNN (ou Réseau de Neurones à Convolution) est un réseau de neurones artificiel qui possède au moins une couche de convolution. Une couche de convolution étant tout simplement une couche dans laquelle on va appliquer un certain nombre de filtres à convolution.

Ok, mais, pourquoi appliquer des filtres à convolution ?

Tout simplement parce qu’une image contient beaucoup, mais alors beaucoup de données en entrée. Imaginez avec une petite image de 100×100 pixels en couleurs … delà nous fait déjà 100x100x3 donc 30 000 données à envoyer dans le réseau de neurones (et c’est une petite image!). Si vous commencez à empiler couches et neurones, très vite le nombre de paramètres de votre réseau va exploser et le nombre de calculs va croitre de manière exponentielle … de quoi mettre par terre votre machine !

Il fallait donc trouver une autre approche que celle classique des réseaux ANN (ou Perceptron Multicouches). L’idée derrière les filtres a convolution est qu’ils permettent de trouver des patterns, des formes dans les images (rappelez vous l’article précédent qui permettait de trouver les contours par exemple). Les CNN permettent en effet de déterminer de manière progressive les différentes formes puis de les assembler pour en trouver d’autres.

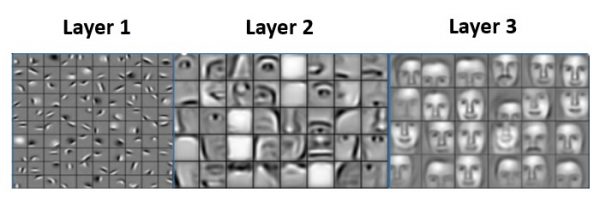
L’exemple classique est que les premières couches d’un tel réseau trouve les formes de base d’un visage: les traits principaux, puis on va détecteur les premières formes: nez, bouche, yeux, etc., puis pour finir le visage et pourquoi pas reconnaître la personne, etc.

Les principaux avantages des filtres à convolution sont:

• Le nombre de paramètres est beaucoup plus petit à trouver comparé à une approche de type ANN. En le réseau de neurones n’aura qu’à trouver les valeurs de la matrice de convolution (kernel) c’est à dire une petite matrice du type 2×2 ou 3×3!
• Les calculs sont extrêmement simples car une convolution ne demande que des multiplications et additions.

Un Réseau de Neurones à Convolution (ou CNN) n’est finalement qu’un réseaux de neurones qui va détecter progressivement les caractéristiques d’une image.

Les couches de convolution du CNN

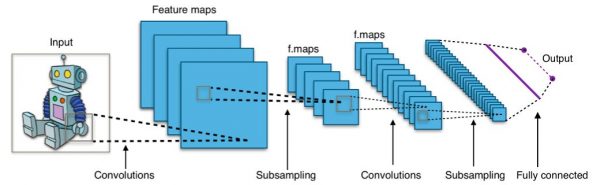
L’architecture d’un tel réseau s’articule très souvent par un empilement de couches convolutives puis de couches denses profondes qui feront le travail de décision. Pour résumer les couches convolutives trouvent les formes et patterns dans l’image et les couches finales effectueront le travail de décision (comme une classification par exemple).

Les couches de convolution comprennent plusieurs filtres. Chaque Filtre de convolution – comme nous l’avons expliqué précédemment – le la même couche va donc extraire ou détecter une caractéristique de l’image. Ainsi à la sortie d’une couche de convolution on a un ensemble de caractéristiques qui sont matérialisées par ce que l’on appelle des features Maps.

Ces caractéristiques (ou images résultantes de filtres à convolution) sont ensuite renvoyées dans d’autres filtres, etc.

Construisons notre CNN avec Tensorflow

Objectif

Pour illustrer les réseaux de neurones convolutif, nous allons créer à partir de zéro le notre qui va nous permettre de classifier des images. Pour ce faire nous utiliserons Python & TensorFlow 2.x (avec keras) et nous allons utiliser un jeu de données classique le MNSIT Fashion.

Description des données

Le jeu de données contient plus de 70000 images en niveau de gris (Cf. ci-dessous):

Chaque image est un carré de 28×28 pixels.

Bonne nouvelle, Tensorflow inclut ses images dans son API donc pas besoin de se fatiguer à récupérer le jeu de données. Pour vous simplifier la vie je vous suggère d’utiliser colab (le notebook sera téléchargeable sur GitHub bien sur).

Ce jeu de données permet d’identifier 10 types d’objets (étiquettes). Ces étiquettes sont codifiées avec des nombres de 0 à 9:

• 0 – T-shirt/haut
• 1 – Pantalon
• 2 – Pullover
• 3 – Robe
• 4 – Manteau
• 5 – Sandale
• 6 – Chemise
• 7 – Sneaker
• 8 – Sac
• 9 – Bottine

Récupération du jeu de données

Commençons par importer les librairies:

import numpy as np
import tensorflow as tf
import matplotlib.pyplot as plt
from tensorflow.keras.layers import Dense, Conv2D, Input, Flatten, Dropout, MaxPooling2D
from tensorflow.keras.models import Model
import pandas as pd
from sklearn.metrics import classification_report,confusion_matrix
from tensorflow.keras.callbacks import EarlyStopping
import seaborn as sns

La récupération du jeu de données ainsi que le découpage se fait très simplement :

dataset_fashion_mnsit = tf.keras.datasets.fashion_mnist
(X_train, y_train), (X_test, y_test) = dataset_fashion_mnsit.load_data()

Maintenant nous avons deux jeux de données (entraînement et test). Regardons la répartition des étiquettes :

pd.DataFrame(y_train)[0].value_counts()

9    6000
8    6000
7    6000
6    6000
5    6000
4    6000
3    6000
2    6000
1    6000
0    6000
Name: 0, dtype: int64

Excellente nouvelle nous avons une répartition très homogène de ces étiquettes.

Préparation des données

Les réseaux de neurones sont très sensibles à la normalisation des données. Dans le cas d’images en niveau de gris c’est très simple et comme les pixels vont de 0 à 255, nous n’avons qu’à diviser tous les pixels par 255:

X_train = X_train / 255
X_test = X_test / 255
print(f"Données entrainement: {X_train.shape}, Test: {X_test.shape}")

Données entrainement: (60000, 28, 28), Test: (10000, 28, 28)

Regardons une image:

plt.imshow(X_train[0])

Et son étiquette:

y_train[0]

9 correspond bien à une botine.

Etant donné que l’on a des images en niveau de gris il nous manque une dimension (couleur : RVB). Rien de grave nous allons l’ajouter …

X_train = X_train.reshape(60000, 28, 28, 1)
X_test = X_test.reshape(10000, 28, 28, 1)

Création du Modèle (réseau de neurones)

Je ne vais pas tout détailler ici, mais on va empiler les couches de notre CNN comme suit :

En Python avec TensorFlow cela donne :

mon_cnn = tf.keras.Sequential()

# 3 couches de convolution, avec Nb filtres progressif 32, 64 puis 128
mon_cnn.add(Conv2D(filters=32, kernel_size=(3,3), input_shape=(28, 28, 1), activation='relu'))
mon_cnn.add(MaxPooling2D(pool_size=(2, 2)))

mon_cnn.add(Conv2D(filters=64, kernel_size=(3,3),input_shape=(28, 28, 1), activation='relu'))
mon_cnn.add(MaxPooling2D(pool_size=(2, 2)))

mon_cnn.add(Conv2D(filters=64, kernel_size=(3,3),input_shape=(28, 28, 1), activation='relu'))
mon_cnn.add(MaxPooling2D(pool_size=(2, 2)))

# remise à plat
mon_cnn.add(Flatten())

# Couche dense classique ANN
mon_cnn.add(Dense(512, activation='relu'))

# Couche de sortie (classes de 0 à 9)
mon_cnn.add(Dense(10, activation='softmax'))

Note: l’explication sur les différents hypermarametres et couches (Conv2D et pooling notamment) viendra dans un article ultérieur.

Afin de ne pas tâtonner sur le nombre d’epochs à réaliser, je vais utiliser la technique de l’earlyStopping qui permet d’arrêter l’apprentissage dés lors que le modèle commence à faire du sur-apprentissage. Celà me permet de négliger ce parametre (epochs).

early_stop = EarlyStopping(monitor='val_loss',patience=2)

Compilons le modèle:

mon_cnn.compile(optimizer='adam',
              loss='sparse_categorical_crossentropy',
              metrics=['accuracy'])
mon_cnn.summary()

Model: "sequential_2"
_________________________________________________________________
Layer (type)                 Output Shape              Param #   
=================================================================
conv2d_2 (Conv2D)            (None, 26, 26, 32)        320       
_________________________________________________________________
max_pooling2d_2 (MaxPooling2 (None, 13, 13, 32)        0         
_________________________________________________________________
conv2d_3 (Conv2D)            (None, 11, 11, 64)        18496     
_________________________________________________________________
max_pooling2d_3 (MaxPooling2 (None, 5, 5, 64)          0         
_________________________________________________________________
conv2d_4 (Conv2D)            (None, 3, 3, 64)          36928     
_________________________________________________________________
max_pooling2d_4 (MaxPooling2 (None, 1, 1, 64)          0         
_________________________________________________________________
flatten (Flatten)            (None, 64)                0         
_________________________________________________________________
dense (Dense)                (None, 512)               33280     
_________________________________________________________________
dense_1 (Dense)              (None, 10)                5130      
=================================================================
Total params: 94,154
Trainable params: 94,154
Non-trainable params: 0

On constate que notre modèle va devoir apprendre 94 154 paramètres, cela va donc prendre quelques minutes lors de la phase d’entrainement.

Entrainement

Lançons l’entrainement. Remarquez le nombre d’epochs (itérations / rétro-propagation) de 25:

mon_cnn.fit(x=X_train, 
            y=y_train, 
            validation_data=(X_test, y_test), 
            epochs=25,
            callbacks=[early_stop])

Epoch 1/25
1875/1875 [==============================] - 59s 31ms/step - loss: 0.7872 - accuracy: 0.7077 - val_loss: 0.4386 - val_accuracy: 0.8408
Epoch 2/25
1875/1875 [==============================] - 58s 31ms/step - loss: 0.4102 - accuracy: 0.8490 - val_loss: 0.3833 - val_accuracy: 0.8625
Epoch 3/25
1875/1875 [==============================] - 58s 31ms/step - loss: 0.3345 - accuracy: 0.8752 - val_loss: 0.3404 - val_accuracy: 0.8740
Epoch 4/25
1875/1875 [==============================] - 58s 31ms/step - loss: 0.2958 - accuracy: 0.8887 - val_loss: 0.3470 - val_accuracy: 0.8747
Epoch 5/25
1875/1875 [==============================] - 58s 31ms/step - loss: 0.2694 - accuracy: 0.8987 - val_loss: 0.3225 - val_accuracy: 0.8844
Epoch 6/25
1875/1875 [==============================] - 58s 31ms/step - loss: 0.2422 - accuracy: 0.9092 - val_loss: 0.3194 - val_accuracy: 0.8862
Epoch 7/25
1875/1875 [==============================] - 57s 31ms/step - loss: 0.2329 - accuracy: 0.9115 - val_loss: 0.3220 - val_accuracy: 0.8851
Epoch 8/25
1875/1875 [==============================] - 58s 31ms/step - loss: 0.2058 - accuracy: 0.9217 - val_loss: 0.3184 - val_accuracy: 0.8898
Epoch 9/25
1875/1875 [==============================] - 58s 31ms/step - loss: 0.1969 - accuracy: 0.9271 - val_loss: 0.3080 - val_accuracy: 0.8962
Epoch 10/25
1875/1875 [==============================] - 58s 31ms/step - loss: 0.1827 - accuracy: 0.9314 - val_loss: 0.3258 - val_accuracy: 0.8890
Epoch 11/25
1875/1875 [==============================] - 58s 31ms/step - loss: 0.1740 - accuracy: 0.9318 - val_loss: 0.3455 - val_accuracy: 0.8878

La condition d’earlystopping permet l’arrêt avant les 25 itérations (arrêt au bout de 11).

Evaluation du modèle

TensorFlow a mis de coté les informations de précision et perte lors de la phase d’entrainement et pour chaque epochs. Il nous suffit de les récupérer:

losses = pd.DataFrame(mon_cnn.history.history)
losses[['accuracy', 'val_accuracy']].plot()

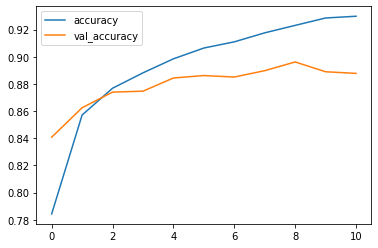
La courbe bleue représente la précision sur les données d’entrainement, l’orange la précision sur les données de test. On remarque d’ailleurs que même si la précision continue de progresser sur les données d’entrainement alors que la précision sur les données de test s’aplatit pour même diminuer. On commence alors à sur-apprendre (over-fitting), c’est pour celà que l’early-stopping à arrêté le processus.

On peut aussi voir la courbe de perte :

losses[['loss', 'val_loss']].plot()

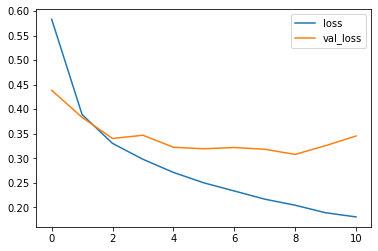
Regardons la matrice de confusion (avec une carte de chaleur avec Seaborn):

plt.figure(figsize=(12,8))
sns.heatmap(confusion_matrix(y_test, pred),annot=True)

On constate qu’il y a des erreurs/confusion surtout entre les chemises (6) et hauts (0), Ce qui n’est pas vraiment étonnant vu la qualité des images.

Prédiction

Essayons notre modèle sur une image. Pour cet essai nous prendrons l’image du début et regardons comment se comporte notre modèle:

img = X_train[0]
mon_cnn.predict(img.reshape(1,28,28,1))

array([[3.9226734e-07, 8.9244217e-08, 6.7499624e-11, 4.7707250e-08,
        1.1513226e-08, 1.3388344e-05, 9.8523687e-09, 7.1390239e-03,
        6.6544054e-08, 9.9284691e-01]], dtype=float32)

Le tableau renvoyé propose en fait une probabilité de résultat pour chaque classe … Pour avoir la plus probable, il suffit de prendre la plus grande valeur :

np.argmax(mon_cnn.predict(img.reshape(1,28,28,1)), axis=-1)[0]

9

Notre modèle marche plutôt pas mal !

Voilà qui clôture cette série sur la gestion des images. Si vous avez apprécié, n’hésitez pas à m’en faire part en commentaire. J’ai bien conscience d’avoir survolé le sujet mais s’était aussi quelque part l’idée … à savoir ne pas trop entrer dans le détail afin de pouvoir se lancer dans ce sujet si passionnant.