Nous avons vu d’une part que les images sont en réalité des matrices a 2 (noir et blanc) ou 3 dimensions (couleurs), nous avons alors vu comment les analyser rapidement grâce aux histogrammes, puis nous avons utilisé ces connaissances pour effectuer des opérations de seuillages sur les images. Nous allons voir dans cet article comment effectuer quelques transformations de bases sur des images avec scikit-image comme la rotation, et changement d’échelle et de taille d’image.
Cet article très simple nous amènera ensuite aux filtres d’images, puis par extension vers les réseaux de neurones à convolution (parties 5 et 6).
Rotation
Avant de voir comment effectuer une rotation d’image simplement avec scikit-image. je vous invite à aller sur le site de skimage pour regarder toutes les transformations d’images que la bibliothèque propose. Il y en a un grand nombre et on n’en verra que certaines dans cet article bien sur. Commençons donc par la rotation.
Avant tout importons les bonnes librairies Python:
import matplotlib.pyplot as plt from skimage.io import imread, imshow from skimage import exposure, transform import matplotlib.pyplot as plt import numpy as np import pandas as pd import math
Ensuite créons un image ultra-simple (4 x 4) composées de pixels noir ou blanc, et affichons la avec la méthode imshow. Nous pourrions utiliser n’importe quel type d’image bien sur mais je trouve qu’un exemple très simple est plus parlant, surtout quand on montre les matrices résultat.
image_test = np.array([[1,0,0,0], [0,1,0,0], [0,1,1,0], [0,0,0,1]])
imshow(image_test, cmap=plt.get_cmap('gray'))
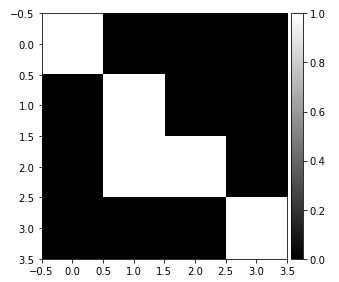
Un simple appel à la fonction transform.rotate() permet donc d’effectuer cette rotation sur l’angle voulu (ci-dessous 90°)
rotated = transform.rotate(image_test, angle=90, preserve_range=True) print(rotated)
array([[0, 0, 0, 1],
[0, 0, 1, 0],
[0, 1, 1, 0],
[0, 0, 0, 0]], dtype=int32)Notez le paramètre preserve_range qui permet de garder la même normalisation de nombre dans la matrice/image.
Visualisons le résultat :
_, axes = plt.subplots(ncols=2)
axes[0].imshow(image_test, cmap=plt.get_cmap('gray'))
axes[1].imshow(rotated, cmap=plt.get_cmap('gray'))
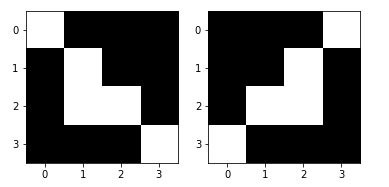
Changement de taille
Changer la taille d’une image est bien sur une opération courante. Imaginons que l’on veuille augmenter la taille de notre image de 4×4 à 6×6. Nous utiliserons pour cela la fonction transform.resize() en lui passant en paramètre le tuple (6,6)
resized_img = transform.resize(image=image_test, output_shape=(6,6), preserve_range=True)
Regardons l’image résultante :
print(resized_img)
array([[0.72222222, 0.5 , 0.13888889, 0.02777778, 0. , 0. ],
[0.5 , 0.5 , 0.41666667, 0.08333333, 0. , 0. ],
[0.16666667, 0.5 , 0.86111111, 0.30555556, 0.08333333, 0.02777778],
[0.16666667, 0.5 , 0.97222222, 0.86111111, 0.41666667, 0.13888889],
[0.08333333, 0.25 , 0.5 , 0.5 , 0.5 , 0.5 ],
[0.02777778, 0.08333333, 0.16666667, 0.16666667, 0.5 , 0.72222222]])Si on explore de plus près ses dimensions, on a bien une image 6×6.
resized_img.shape
(6, 6)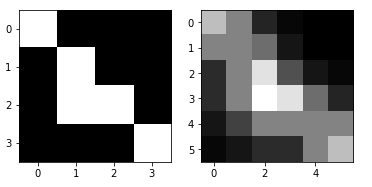
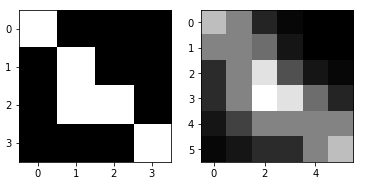
Vous avez sans doute remarqué que nous avons dorénavant des nombres décimaux dans la matrice (donc des niveaux de gris). Celà est en fait dû à l’agrandissement. Repassons en pur noir et blanc pour avoir notre véritable agrandissement. Pour celà nous allons convertir les valeurs > 0,5 en 1 et les autres en zéro:
intresized = resized_img > 0.5
imshow(intresized.astype('int32'), cmap=plt.get_cmap('gray'))
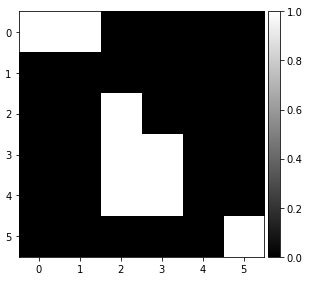
On voit mieux maintenant notre étirement d’image avec la forme du milieu et celle du haut à gauche.
Changement d’échelle
Pour changer le grossissement d’une image on pourra utiliser transform.rescale(). Ci-dessous nous utilisons un ratio de 1/2:
image_rescaled = transform.rescale(image=image_test, scale=1.0 / 2.0, anti_aliasing=False, preserve_range=True)
_, axes = plt.subplots(ncols=2)
axes[0].imshow(image_test, cmap=plt.get_cmap('gray'))
axes[1].imshow(image_rescaled, cmap=plt.get_cmap('gray'))
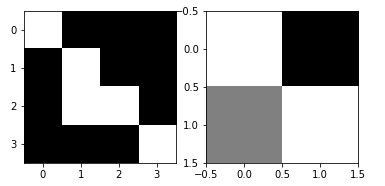
Transformations euclidiennes
La librairie scikit-image permet d’effectuer vraiment un grand nombre de transformations sur des images. Je trouve la transformation SimilarityTransform() particulièrement utile car elle permet de combiner des transformations euclidiennes (translations) avec du changement d’echelle.
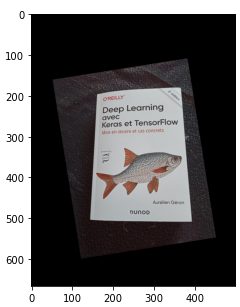
Prenons une image normale cette fois-ci, l’image n’est pas droite et nous allons la redresser, puis la décaler directement avec cette fonction
image = imread('book.jpg')
imshow(image)

tr = transform.SimilarityTransform(scale=1.5, rotation=math.pi/20, translation=(-40, -250)) plt.figure(figsize=(8, 5)) image_tr_1 = transform.warp(image, tr) plt.imshow(image_tr_1)
En fait la rotation de l’image créé un décalage que nous corrigeons avec le parametre translation ci-dessus.
Voici qui cloture cet article sur les transformations de bases d’image. Nous allons dans les prochains articles aborder les filtres et notament ceux de convolution qui nous permettrons de mieux comprendre comment les réseaux de neurones dit convolutifs sont devenus aussi omniprésents dans le monde du traitement de l’image.
Ingénieur en informatique avec plus de 20 ans d’expérience dans la gestion et l’utilisation de données, Benoit CAYLA a mis son expertise au profit de projets très variés tels que l’intégration, la gouvernance, l’analyse, l’IA, la mise en place de MDM ou de solution PIM pour le compte de diverses entreprises spécialisées dans la donnée (dont IBM, Informatica et Tableau). Ces riches expériences l’ont naturellement conduit à intervenir dans des projets de plus grande envergure autour de la gestion et de la valorisation des données, et ce principalement dans des secteurs d’activités tels que l’industrie, la grande distribution, l’assurance et la finance. Également, passionné d’IA (Machine Learning, NLP et Deep Learning), l’auteur a rejoint Blue Prism en 2019 et travaille aujourd’hui en tant qu’expert data/IA et processus. Son sens pédagogique ainsi que son expertise l’ont aussi amené à animer un blog en français (datacorner.fr) ayant pour but de montrer comment comprendre, analyser et utiliser ses données le plus simplement possible.



Bonjour,
Cette série d’article est très intéressante. Par contre incluez vous la dilation et l’érosion dans les transformations de base, car je pense que cela ne fait pas partie des filtre. Ce sont néanmoins des opérations très utiles.
Bonjour,
Vous avez raison d’une certaine manière. Mais à vrai dire, dilatation et érosion sont considérés comme des filtres non linéaires (cf. transformations morphologiques) bref si on est puriste on mettra ces transformations plutot dans les filtres. Ça sera chose faite dans le prochain article de la série.
Benoit