C’est bientôt la rentrée, il a fait chaud, la plage a été bonne et le sable bien chaud. Vous êtes donc bien reposé et prêt à attaquer la rentrée. C’est donc le bon moment pour remettre à plat quelques bases de statistiques qui vous permettront de mieux comprendre et utiliser les algorithmes de Machine Learning. Ne faites pas la grimace, c’est pour la bonne cause 🙂
Je vous propose dans cet article de passer en revue le petit bagage indispensable de tout bon bon Data-Scientiste :
- Moyenne
- Médiane
- Ecart type
- Variance
- Quantile
- Quartile
La moyenne
Vous savez tous ce qu’est la moyenne ? oui sans doute, néanmoins nous allons quand même la redéfinir surtout pour la mettre en perspective avec la notion de médiane que nous verrons plus loin.
La moyenne se définit donc par la somme des données divisée par le nombre de données. Soit d’un point de vue mathématique :
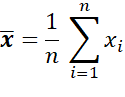
Prenons un exemple maintenant avec une petite distribution de valeurs = [1, 7, 8, 9, 10], la moyenne est évidemment 7.
Vue dans une perspective graphique ramenons l’axe des ordonnées à la valeur moyenne pour mieux la visualiser. Et bien c’est comme si la surface des valeurs dessus et dessous cette moyenne était égale.
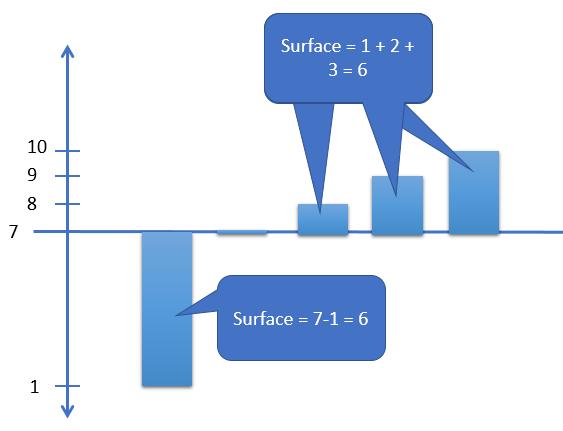
La médiane
Attention à la confusion ! car médiane ne signifie pas du tout moyenne (même si ces deux valeurs peuvent être égales. Par définition la médiane est la valeur d’une distribution qui permet de découper en deux parties égales cette même distribution.
Si on reprend notre distribution précédente, on aura pour valeur médiane 8 :

En fait le calcul est plutot évident dés lors que nous avons un nombre impair de valeur dans notre distribution.
Par contre si nous avons un nombre de valeurs est paire, la médiane est la moyenne des deux valeurs du milieu.
Ecart type
L’écart type (standard deviation en anglais), aussi orthographié écart-type, est une notion mathématique définie en probabilités et appliquée à la statistique. En probabilité, l’écart type est une mesure de la dispersion d’une variable aléatoire; en statistique, il est une mesure de dispersion de données. Il est défini comme la racine carrée de la variance ou, de manière équivalente, comme la moyenne quadratique des écarts par rapport à la moyenne. Il a la même dimension que la variable aléatoire ou la variable statistique en question.
Les écarts types sont rencontrés dans tous les domaines où sont appliquées les probabilités et la statistique, en particulier dans le domaine des sondages, en physique, en biologie ou dans la finance. Ils permettent en général de synthétiser les résultats numériques d’une expérience répétée. Tant en probabilités qu’en statistique, il sert à l’expression d’autres notions importantes comme le coefficient de corrélation, le coefficient de variation ou la répartition optimale de Neyman.
L’écart type sert à mesurer la dispersion d’un ensemble de données autour de la moyenne. Plus il est faible, plus les valeurs sont regroupées autour de la moyenne.
Exemple de deux échantillons ayant la même moyenne mais des écarts types différents illustrant l’écart type comme mesure de la dispersion autour de la moyenne:

(Source Wikipédia)
L’écart-type est donc une mesure qui permet de mesurer la dispersion des données dans une distribution.
Cette mesure consiste à calculer la distance des points par rapports à la moyenne.
Afin de mieux comprendre cette mesure, regardez comment on la calcule d’un point de vue pratique en 5 étapes simples :
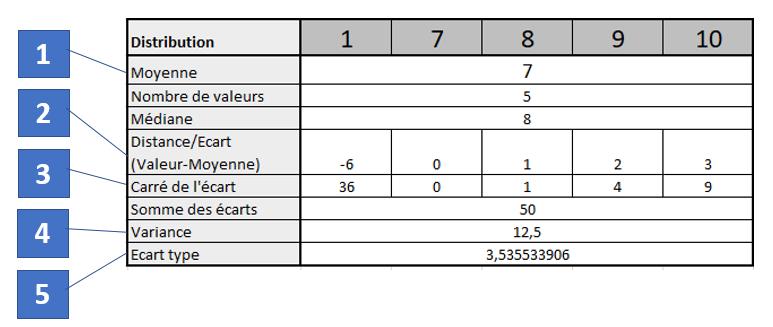
Étapes :
- Calcul de la moyenne de la distribution (ici la moyenne est égale à 7).
- Calcul de la distance entre la moyenne et chaque valeur de la distribution (une simple soustraction)
- Mise au carré de la distance calculée précédemment
- Calcul de la variance : C’est la somme des écarts au carré calculés précédemment divisé par le nombre de valeurs dans la distribution moins 1.
- Calcul de l’écart type : c’est simplement la racine carrée de la variance.
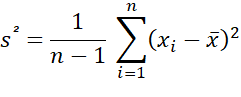
D’un point de vue analytique voici la formule de calcul :
Variance
Nous venons de le voir la variance est tout simplement le carré de l’écart type.
Quantile
Nous avons vu que la médiane permettait de découper une distribution en deux parties égales. Et bien les quantiles ne sont qu’une généralisation de cette idée de découper une distribution en parts. L’idée sous-jacente est donc de créer des découpages à nombre de valeurs égales dans cette distribution.

D’un point de vue vocabulaire :
- La médiane sépare les valeurs en deux groupes de population égale .
- Les quartiles les séparent en quatre groupes.
- et d’un point de vue global : les quantiles en n.
NB: il existe aussi les centiles et déciles.
Quartile
Les quartiles sont donc les trois quantiles qui divisent un ensemble de données en quatre groupes de taille égale. La médiane quant à elle est le quantile qui sépare le jeu de données en deux groupes de taille égale.
D’un point de vue pratique (Q1 = 1er quartile, Q3 = 3ème quartile):
- Un quart des valeurs sont inférieures ou égales à Q1.
- Les trois quarts des valeurs sont inférieures ou égales à Q3.
- La moitié des valeurs se trouvent dans l’intervalle interquartile [Q1 ; Q3].
Ingénieur en informatique avec plus de 20 ans d’expérience dans la gestion et l’utilisation de données, Benoit CAYLA a mis son expertise au profit de projets très variés tels que l’intégration, la gouvernance, l’analyse, l’IA, la mise en place de MDM ou de solution PIM pour le compte de diverses entreprises spécialisées dans la donnée (dont IBM, Informatica et Tableau). Ces riches expériences l’ont naturellement conduit à intervenir dans des projets de plus grande envergure autour de la gestion et de la valorisation des données, et ce principalement dans des secteurs d’activités tels que l’industrie, la grande distribution, l’assurance et la finance. Également, passionné d’IA (Machine Learning, NLP et Deep Learning), l’auteur a rejoint Blue Prism en 2019 et travaille aujourd’hui en tant qu’expert data/IA et processus. Son sens pédagogique ainsi que son expertise l’ont aussi amené à animer un blog en français (datacorner.fr) ayant pour but de montrer comment comprendre, analyser et utiliser ses données le plus simplement possible.


4 Replies to “Bagage minimal de statistiques pour le Machine Learning”