Biais & Variance … dilemme ou compromis ?

Introduction

Dés lors que vous allez commencer à mettre au point des modèles de Machine Learning vous aller vous confronter au délicat problème d’équilibre dans l’ajustement du biais et de la variance. Trouver ce fameux équilibre est l’ingrédient principal d’un bon modèle.

Malheureusement il n’y a pas de recette miracle. La connaissance, l’expérience et même l’intuition vous aiderons dans cette tâche difficile mais oh combien passionnante. Cela dit, je ne vais pas me focaliser dans cet article sur les méthodes d’ajustements de ces deux indicateurs essentiels mais plutôt sur leur signification.

Alors compromis ou dilemme entre ces deux indicateurs incontournables ? tout d’abord voyons de quoi il s’agit exactement.

Qu’est-ce que le biais ?

Le biais mesure en quelque sorte l’erreur. Quand on fait du Machine Learning on n’est pas en train de rechercher une règle qui va répondre à 100% de manière exacte à un problème donné. De toute façon trouver une telle règle est illusoire car les données qui nourrissent les modèles ne sont pas elle non plus totalement exactes.

Bref, l’apprentissage par les données d’expérience se fait donc par l’ajustement progressif d’un modèle (supervisé). Et l’ajustement de ce modèle est lui-même réalisé par la minimisation de l’erreur entre ce que peut produire le modèle par rapport la valeur réelle.

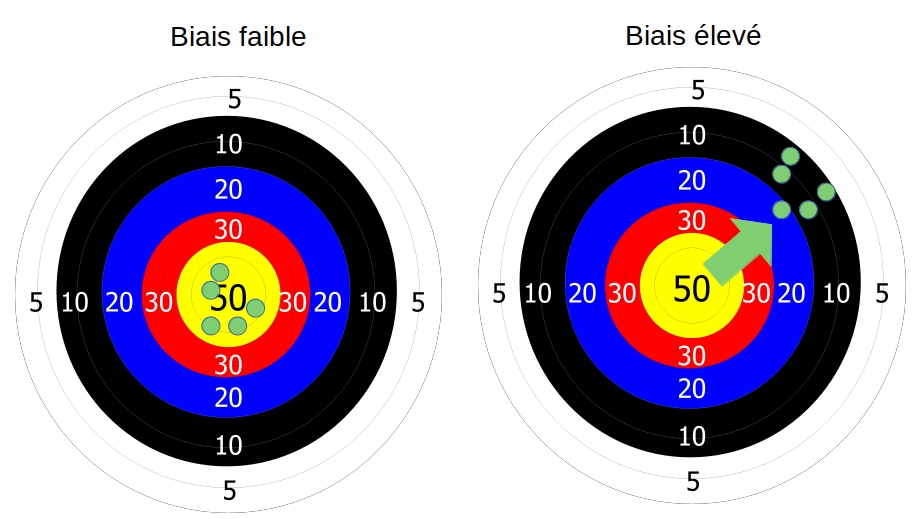
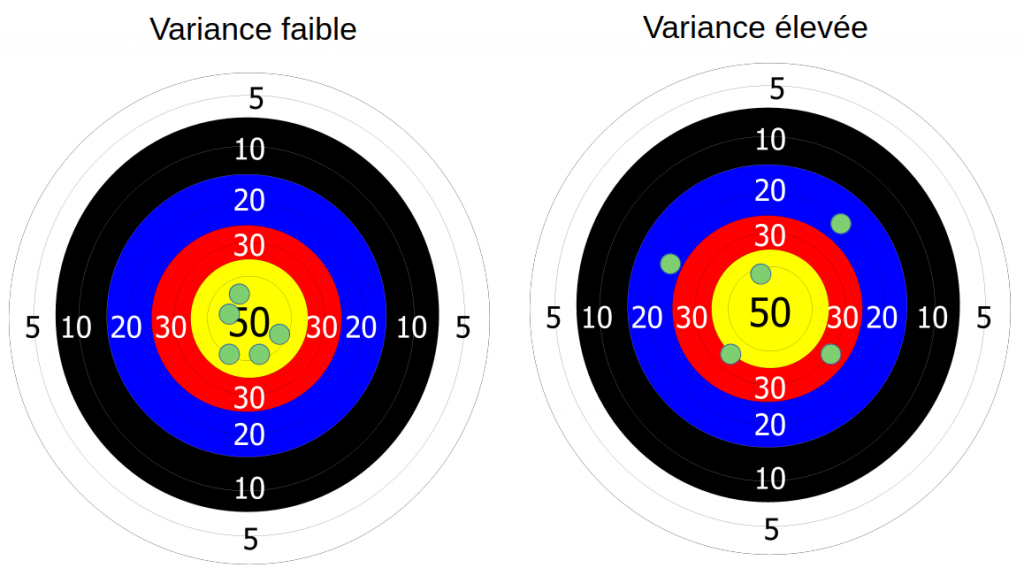
Afin d’illustrer mon propos, j’aime utiliser l’image d’une cible en tir à l’arc :

Imaginons que vous tiriez à l’arc, et qu’il y a du pas mal vent. Néanmoins vous êtes à l’abri et vous n’avez pas senti ce vent. Vous faites vos tirs, et surprise, ils sont tous décalés comme dans l’image ci-dessus à droite.

Et bien ce paramètre vent que vous n’avez pas pris en compte lors de vos tirs c’est votre biais. Et ce biais provoque un décalage gênant dans votre résultat.

D’accord, mais le biais dans le Machine Learning ?

Dans le monde du Machine Learning, on est sans arrêt en train de calculer les erreurs (comment faire une descente de gradient sinon ?), on est surtout toujours en quête de la minimiser au maximum (même si c’est parfois pas la bonne chose comme on va le voir ensuite).

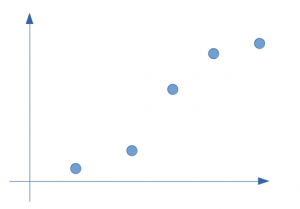
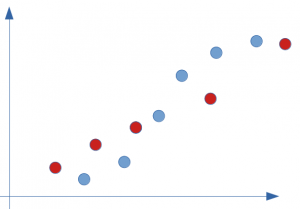
Prenons un exemple simple de répartition sur quelques points seulement comme ci-dessous :

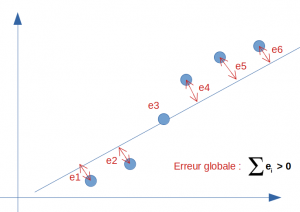
A vue d’oeil une régression linaire répond partiellement à ce type de problème. Regardons dans cette hypothèse la droite et calculons son erreur par rapport à la réalité (la valeur réelle constatée dans notre modélisation supervisée) :

L’erreur globale (ou le biais) n’est bien sur pas nulle car la droite ne peut pas passer par tous les points en même temps. On a donc un biais plus ou moins élevé sur ce modèle. Disons que nous aurions un score de 95%.

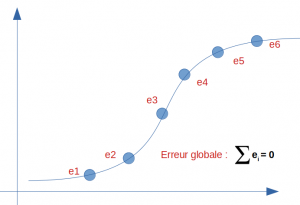
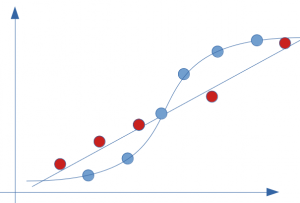
Et si maintenant nous faisions du zèle et que nous trouvions le modèle idéal pour cette répartition ? regardez le résultat ci-dessous, l’erreur et donc le biais se trouve nul :

Nous avons donc un score 100%. C’est vraiment mieux n’est-ce pas ? Alors mission accomplie ? du coté du biais oui … mais n’est-on pas allé trop loin ? nous allons voir maintenant du coté d’un autre indicateur important: la variance si notre modèle est si bon que ça.

La variance

La variance sert à mesurer la dispersion d’une liste de valeurs. Si on reprend notre image du tir à l’arc. Nous avons maintenant pris en compte le vent mais par contre nous avons oublié nos lunettes (certes ce n’est pas vraiment pratique surtout quand on est myope pour aller faire du tir à l’arc). Voyant flou il y a de fortes chance que notre résultat ressemble à cela :

Les flèches sont dispersées autour du centre (en statistique, pour la variance on parle de dispersion autour de la moyenne).

Et la variance dans le Machine Learning ?

Nous avons vu dans notre exemple précédent que nous avons minimisé au maximum le biais (à nul). Attention cependant car nous avons fait ce modèle sur un jeu de données d’entrainement … regardons ce que ce modèle donnerait avec le jeu de données de test (points rouge) :

Si on applique le modèle précédent dont le score était je vous le rappelle 100%, et que l’on calcul l’erreur, on constate surtout que le le biais est loin d’être nul :

Il est même fort probable que le score soit maintenant assez catastrophique car l’erreur est sans doute supérieure à celle de notre bonne vieille droite (régression linaire) :

En fait voici l’illustration de ce qu’est un sur-apprentissage (overfit), la plaie des Data-scientistes.

Conclusion

Si le biais permet de calculer l’erreur d’un modèle, la variance elle permet d’en calculer la résilience, c’est à dire sa capacité à se généraliser. L’enjeu est donc de trouver un bon compromis entre une erreur acceptable et une bonne capacité de généralisation … car en effet la perfection n’est pas possible pour les deux comme nous venons de le voir. Il n’est donc pas question de dilemme (ou de choix) dans la mesure où ces deux indicateurs doivent êtres ajustés ensemble pour avoir un bon modèle !

La seule chose qui n’est pas vraiment pratique est qu’on ne peut pas ajuster ces deux paramètres simultanément. Il faut tout d’abord concevoir le modèle (sans être trop gourmand du coup), puis ensuite le tester sur d’autres jeux de données. Cela prend donc du temps, et de la patience … une autre vertu du data-scientiste 😉