Introduction
Les chaînes de Markov sont quelque peu délaissée depuis l’apparition des algorithmes de Machine Learning. Pourtant elles restent toujours assez utilisées notamment pour les prévisions météo et même pour la complétion lorsque vous faites une recherche dans Google.
La philosophie ainsi que la mise en œuvre sont en effet assez simple. Nous allons voir dans cet article sur un cas extrêmement simple comment modéliser ce type d’algorithme mais aussi comment l’utiliser avec Python.
Tout d’abord pas besoin de se lancer dans un premier temps dans de grandes équations mathématiques. L’idée des chaînes de Markov est de décrire dans un premier temps une séquence d’état. Pour la météo par exemple on fera une suite de constat comme :
- J+0 : Beau temps
- J+1: Pluie
- J+2 : Pluie
- J+3 : Beau temps
- etc.
- J+n : Nuageux
Cette série de constat est une séquence, chaque étape d’une séquence indique un état. Avec les chaînes de Markov, nous allons dans un premier temps dessiner ce constat. L’idée est en suite très simple, partant d’un ou plusieurs constat nous allons définir les probabilités de transition entre chaque état. Ces probabilités cartographiées et référencées nous permettrons ensuite de définir nos prévisions. Simple non ? voyons ce que cela va donner sur un cas concret.
Cas concret : Les positions du chat !
Changeons de sujet (météo) et faisons une expérience ensemble. Imaginons que nous regardons notre chat et que toutes les 5 minutes on note sa posture. Cela pourrait donner cette séquence de constat :
- Minute 1 : Debout (sur ses 4 pattes 😉 )
- Minute 5 : Assis
- Minute 10 : Assis
- etc.
- Minute 40 : Assis
D’un point de vue séquentiel cela pourrait être présenté comme cela :

Ce qui est intéressant est maintenant de montrer cette même séquence sous l’angle des états. Pour cela on va créer un rond pour chaque état et nous allons relier ces états par rapport à ceux constatés dans notre séquence :
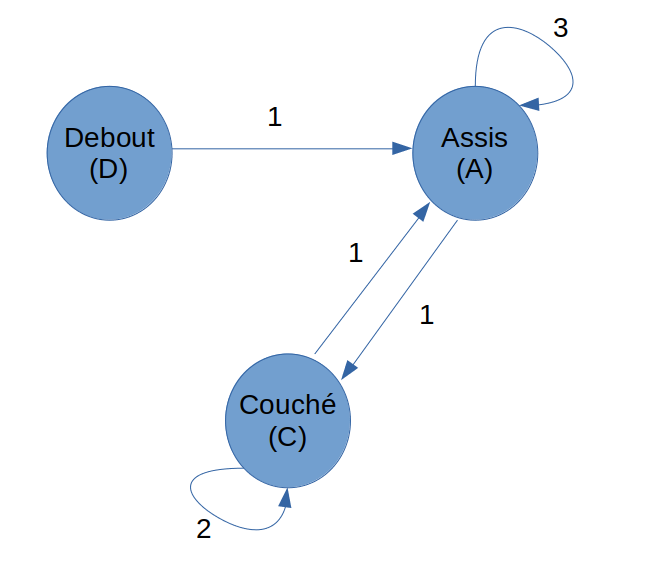
Ce qui est intéressant avec ce type de diagramme c’est qu’il est plus simple à regarder et à comprendre car il n’y a plus de redondance d’état.
Une caractéristique importante des chaînes de Markov est que son principe est basé sur un état et non sur un historique d’état. Une chaîne de Markov est une suite de variables aléatoires: le futur ne dépend pas du passé, ou autrement dit le futur ne dépend du passé que par le présent.
Un autre point important c’est que les chaînes de Markov sont basées sur des probabilités. L’idée est de définir une matrice de probabilité (dite matrice de transition) qui va nous permettre de calculer une prévision sur les étapes suivantes.
Calculons les probabilités des positions de notre chat
C’est très simple en fait. Dans le diagramme suivant on note la probabilité du passage de l’état C (couché) à l’état D (Debout) de cette manière :
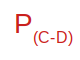
On appelle cette probabilité la probabilité de transition d’un pas du processus.
Par rapport aux possibilités constatées pendant l’expérience nous aurons les probabilités suivantes :
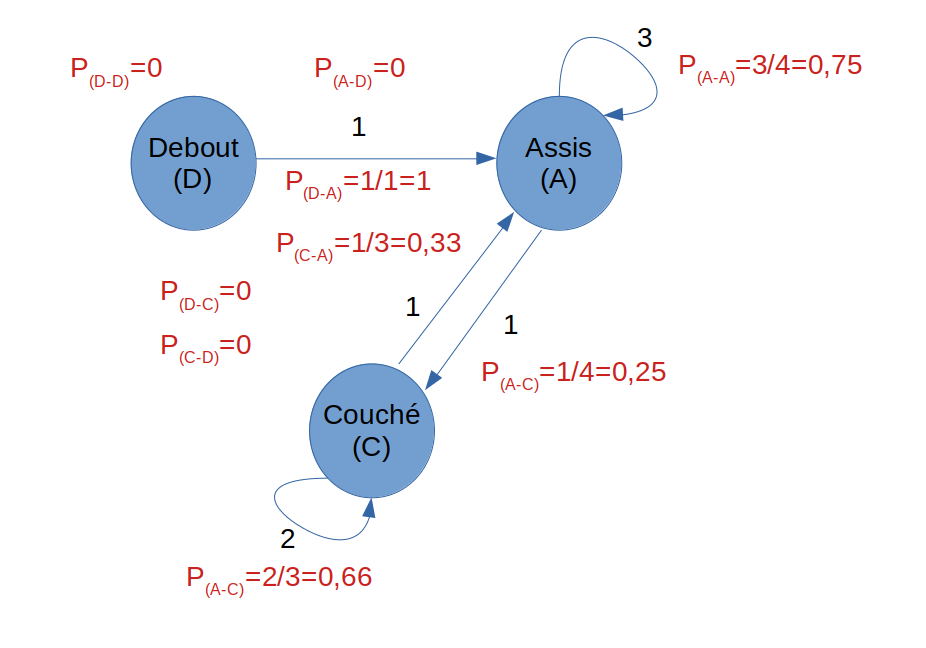
Par exemple : La probabilité de passer de l’état Couché (C) à l’état Assis (A) est de 2 sur 3 (soit 0,66). Nous avons en effet 2 flèches qui bouclent sur l’état C et une flèche qui va vers A : soit 3 possibilités au total de changement d’état.
La matrice de transition
Une fois que toutes les probabilités de changement d’état ont été définies/calculées on peut les représenter sous forme de matrice (Matrice de transition). Nous aurons une matrice carrée de 3×3 car nous avons 3 états que nous allons écrire comme suit :
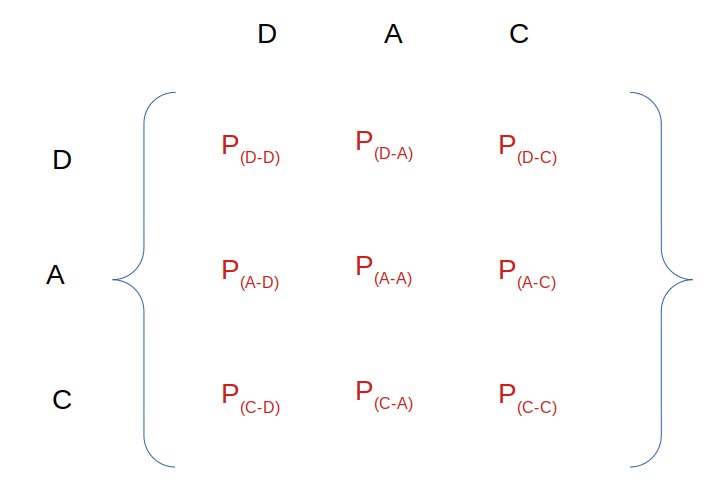
Soit la matrice numérique suivante :
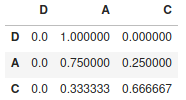
Cette matrice va nous permettre de calculer simplement la prévision de passage d’une étape 1 à une étape 2. Puis en re-multipliant par cette matrice (de transition) nous pourrons pas extension trouver l’état (enfin la prédiction de l’état) n+1.
Qu’est-ce que ça donne en Python ?
On pourrait calculer des multiplications de matrice à la main (avec numpy par exemple) et gérer assez simplement les transitions. Ce qui est vraiment bien avec Python c’est qu’il y a des librairies pour tout. Pourquoi se fatiguer donc ?
Je vais importer la librairie marc qui va me faire tout le travail que nous avons vu jusque là.
pip install marc
Une fois la librairie importée/installée, nous n’avons qu’à décrire notre séquence de toute à l’heure :
from marc import MarkovChain
import pandas as pd
sequence = [
'D', 'A', 'A',
'A', 'C', 'C',
'C', 'A', 'A'
]
chaine = MarkovChain(sequence)
La séquence est décrite dans une liste Python qui se nomme séquence. L’appel à la fonction MarkovChain() permet de faire tous les calculs que nous avons vu précédemment.
La matrice est calculée, il ne reste qu’à l’afficher :
chaine.matrix
[[0.0, 1.0, 0.0],
[0.0, 0.75, 0.25],
[0.0, 0.3333333333333333, 0.6666666666666666]]Bien sur la librairie ne s’arrête pas là, vous pouvez calculer la prochaine (probable) étape :
chaine.next('A')
'A'Et pourquoi pas les 20 prochaines …
chaine.next('D', n=20)
['A',
'A',
'A',
'A',
'A',
'A',
'A',
'A',
'A',
'A',
'C',
'C',
'C',
'A',
'C',
'C',
'C',
'A',
'A',
'C']Conclusion
Les chaînes de Markov ne sont en effet pas jeunes (Andreï Markov a publié les premiers résultats sur les chaînes de Markov en 1906) mais restent néanmoins très pertinentes dés lors que nous avons à faire à des processus stochastiques. Personnellement je les trouve très simple et parfois même complémentaires d’algorithmes de Machine Learning classiques (arbres de décision, boost, bayes, etc.). En fait les champs d’applications sont multiples : écrire du texte ou de la musique, prévisions météos, etc.
Bref un algorithme à ne pas mettre de coté même si il peut paraître quelque peu démodé ! Vous avez besoin d’un algorithme qui vous permet suite à une séquence d’action de prédire la suivante … jetez un œil sur cet Algorithme !
Ingénieur en informatique avec plus de 20 ans d’expérience dans la gestion et l’utilisation de données, Benoit CAYLA a mis son expertise au profit de projets très variés tels que l’intégration, la gouvernance, l’analyse, l’IA, la mise en place de MDM ou de solution PIM pour le compte de diverses entreprises spécialisées dans la donnée (dont IBM, Informatica et Tableau). Ces riches expériences l’ont naturellement conduit à intervenir dans des projets de plus grande envergure autour de la gestion et de la valorisation des données, et ce principalement dans des secteurs d’activités tels que l’industrie, la grande distribution, l’assurance et la finance. Également, passionné d’IA (Machine Learning, NLP et Deep Learning), l’auteur a rejoint Blue Prism en 2019 et travaille aujourd’hui en tant qu’expert data/IA et processus. Son sens pédagogique ainsi que son expertise l’ont aussi amené à animer un blog en français (datacorner.fr) ayant pour but de montrer comment comprendre, analyser et utiliser ses données le plus simplement possible.

effectivement!!! le problème est qu’il ne prend en compte le passé! sinon très beau cours